… czyli co to jest i skąd się bierze moc i moment obrotowy oraz czy lepsza jest moc z obrotów, czy z momentu, a więc o silnikach wysoko- i wolnoobrotowych.

O mocy i momencie powiedziano już dużo, jednak z wielu tych wypowiedzi odnieść można wrażenie, że autor sam do końca nie wie o czym pisze – stosuje uogólnienia, zbyt daleko idące porównania. Zatem rozwiążę raz na zawsze tą kwestię, sięgając aż do objętości i temperatury zapalonej mieszanki paliwowo-powietrznej.

A więc najbardziej precyzyjnie – co to jest i skąd pochodzi moc i moment obrotowy?

Zgodnie z definicją moc jest ilością pracy wykonaną w jednostce czasu:
$P = \frac{W}{t}$
P – moc (W)
W – praca (J)
t – czas (s)

a praca to iloczyn siły i przemieszczenia:
$W = F \cdot s$
W – praca (J)
F – siła (N)
s – przemieszczenie (m)

Łącząc te wzory ze sobą otrzymamy:
$P = F \cdot \frac{s}{t}$

Czyli moc to iloczyn siły działającej na wał korbowy i przemieszczenia punktu przyłożenia tej siły w jednostce czasu.

Nie znamy siły działającej na wał korbowy, jednak znany jest moment obrotowy na nim. Określa on średnią wartość siły w ciągu pełnego cyklu pracy silnika działającą na ramię o długości 1 metra. Moment obrotowy silnika można zdefiniować jako iloczyn siły działającej na tłok i głębokości wykorbienia wału korbowego:
$M = F \cdot r$
M – moment obrotowy (Nm)
F – siła (N)
r – głębokość wykorbienia wału korbowego (m)

A więc nieznaną nam siłę można zastąpić wzorem:
$F = \frac{M}{r}$

Zatem wzór na moc przyjmuje postać:
$P = \frac{M}{r} \cdot \frac{s}{t}$

Wał korbowy wykonuje ruch obrotowy, a więc droga punktu przyłożenia siły (s) to α (kąt obrotu w radianach) * r:
$s = \alpha \cdot r$

Kąt obrotu wynosi 360*, a więc:
$\alpha = 2 \cdot \pi \approx 6,28 \; rad$

Zatem:
$s = 2 \cdot \pi \cdot r = 6,28 \; rad \cdot r$

t jest czasem, w jakim wał korbowy wykonuje pełen obrót:
$t = \frac{1}{f}$

Zamiast s dzielić przez t, wygodniej pomnożyć przez odwrotność t, a więc przez prędkość obrotową silnika wyrażoną w obrotach na sekundę:
$\frac{1}{t} = f$

Podstawiając do wzoru:
$P = \frac{M}{r} \cdot \alpha \cdot r \cdot f$ – r ulega skróceniu
$P = M \cdot \alpha \cdot f$
$P = M \cdot 6,28 \; rad \cdot f$

Zatem moc zależy od momentu obrotowego i prędkości obrotowej silnika. Wartość momentu obrotowego (M) to po prostu iloczyn siły działającej na wał korbowy, przekazanej przez tłok (F) i głębokości wykorbienia wału korbowego (r). Większe wykorbienie, to większe ramię siły, które powoduje zwiększenie wartości momentu obrotowego.

Pojedynek, źródło: Internet

Siła działająca na tłok

Siła działająca na tłok zależy od ciśnienia panującego w cylindrze oraz od powierzchni tłoka, a więc od jego średnicy, gdyż ciśnienie to siła działająca na jednostkę powierzchni:
$F = \rho \cdot S$
F – siła (N)
p – ciśnienie ( $Pa = \frac{N}{m^2}$ )
S – powierzchnia ( $m^2$ )

W 1834 roku Benoît Clapeyron sformułował równanie stanu gazu doskonałego:
$\rho \cdot V = n \cdot R \cdot T$
p – ciśnienie ( $Pa, \;\;\; \frac{N}{m^2}$ )
V – objętość ( $m^3$ )
n – liczba moli gazu (mol)
R – uniwersalna stała gazowa ( $R= 8,314 \; \frac{J}{mol \cdot K}$ )
T – temperatura (K)

Opisuje ono związek pomiędzy ciśnieniem, objętością i temperaturą gazu doskonałego. Dla danej porcji gazu iloczyn n i R stanowi stałą, która określa zależność pomiędzy zmiennymi:
$\frac{p \cdot V}{T} = const.$

Czyli:

jeśli objętość rośnie to maleje ciśnienie i temperatura – suw ssania – przy otwartych zaworach następuje wyrównanie ciśnienia z ciśnieniem atmosferycznym
jeśli objętość maleje to rośnie ciśnienie i temperatura – suw sprężania
zapłon paliwa powodujący dodatkowy wzrost temperatury, który powoduje również wzrost ciśnienia skutkujący wzrostem objętości
jeśli objętość rośnie to maleje ciśnienie i temperatura – suw pracy
jeśli objętość maleje to rośnie ciśnienie i temperatura – suw wydechu – przy otwartych zaworach następuje wyrównanie ciśnienia w cylindrze z ciśnieniem w układzie wydechowym

Przekształcając wzór otrzymamy, że ciśnienie to:
$\rho = \frac{n \cdot R \cdot T}{V}$

Czyli siła działająca na tłok jest równa:
$F = \frac{n \cdot R \cdot T}{V} \cdot S$

Tłok jest okrągły, a więc jego powierzchnię wyraża wzór:
$S = \pi \cdot (r_{tloka})^2$
S – Pole powierzchni ( $m^{2}$ )
r_tłoka – promień tłoka (m)

Podsumowując siła działająca na tłok to:
$F = \frac{n \cdot R \cdot T}{V} \cdot \pi \cdot (r_{tloka})^2$

Moment obrotowy silnika to:
$M = F \cdot r = \frac{n \cdot R \cdot T}{V} \cdot \pi \cdot (r_{tloka})^2 \cdot r$
przy założeniu, że weźmiemy średnią wartość elementów z równania Clapeyrona.

Moc silnika to:
$P = \frac{n \cdot R \cdot T}{V} \cdot \pi \cdot (r_{tloka})^2 \cdot r\cdot 6,28 \; rad \cdot f$

Powietrza nigdy mało, źródło: Internet

Praca silnika

Przy zapłonie mieszanki paliwowo-powietrznej, kiedy tłok jest w górnym położeniu, dysponujemy minimalną objętością i maksymalną temperaturą, a więc ciśnienie jest największe. Zapłon paliwa powoduje dodatkowe zwiększenie temperatury, a przez to ciśnienia w cylindrze. W miarę ruchu tłoka w dół, temperatura maleje, a objętość rośnie, co powoduje spadek ciśnienia. A więc mamy dwie skrajne wartości objętości cylindra w suwie pracy:

objętość minimalna
objętość maksymalna

Objętość komory spalania zmienia tłok, poruszając się w dół podczas suwu pracy. Projektując silnik o danej pojemności, zwiększając średnicę tłoka musimy zmniejszyć jego skok, aby objętość maksymalna pozostała niezmieniona. Podobnie przy zwiększaniu skoku tłoka – musimy zmniejszyć średnicę. Wiecie, które rozwiązanie charakteryzuje silniki wysoko- i wolnoobrotowe? Silniki wysokoobrotowe mają dużą średnicę tłoka, który krótkimi skokami przemieszcza się w górę i w dół. Silniki wolnoobrotowe mają małą średnicę, ale tłok pokonuje dłuższą drogę.

Wracając do meritum można przyjąć założenie, że skoro moc zależy od iloczynu wartości momentu obrotowego i prędkości obrotowej silnika ( $P = M \cdot 6,28 \; rad \cdot f$ ), a wartość momentu obrotowego zależy od ilości mieszanki paliwowo-powietrznej, to moc w przybliżeniu jest proporcjonalna do ilości spalanego paliwa. Czyli uogólniając moc to ilość paliwa spalanego w jednostce czasu przy założeniu, że silnik ma stałą sprawność w użytecznym zakresie obrotów, a więc ma płaski przebieg momentu obrotowego.

Wobec tego istnieją dwie podstawowe (poza doładowaniem) możliwości na zwiększenie ilości spalanego paliwa w jednostce czasu:

Zwiększenie prędkości obrotowej silnika, przez co w jednostce czasu cylindry napełniane są częściej mieszanką paliwowo-powietrzną. Są to silniki wysokoobrotowe. Charakteryzuje je współczynnik kształtu cylindra, czyli stosunek średnicy do skoku tłoka mniejszy niż 1.
Zwiększenie pojemności silnika, dzięki czemu mimo mniejszej prędkości obrotowej objętość spalanej mieszanki paliwowo-powietrznej jest większa. Są to silniki wolnoobrotowe o stosunku średnicy do skoku tłoka większym niż 1.

Wartość rozdzielająca silniki wysoko- od niskoobrotowych została przyjęta umownie, więc nie można na tej podstawie jednoznacznie klasyfikować silnika.

Chevrolet Corvette C3, źródło: Internet

Obroty czy pojemność?

A więc lepszy mały silnik, nadrabiający swoją wielkość obrotami, czy wolnoobrotowy olbrzym?

Przewagą małolitrażowego silnika jest jego mniejsza waga oraz mniejsze wymiary. Jednak koszty jego produkcji wcale nie muszą być mniejsze – trudność w zaprojektowaniu, precyzja wykonania, redukcja masy będącej w ruchu, duże obciążenie korbowodu i wału korbowego, wzrost obciążeń cieplnych i mechanicznych oraz skomplikowany układ dolotowy wraz z układem rozrządu – to wszystko wpływa na jego cenę. Plusem jest to, że większa średnica tłoka pozwala zastosować zawory o większej średnicy, co ułatwia wymianę ładunku.

Duży silnik możne być znacznie bardziej toporny i prosty. W końcu to z pojemności brała się moc kilkadziesiąt lat temu, kiedy technologia nie pozwalała na zbyt wiele. Ma on większą masę i wymiary, jednak jest mniej wymagający w budowie, dzięki czemu może być tańszy. Obciążenia cieplne są mniejsze, gdyż ciepło wymieniane jest na większej powierzchni, dzięki czemu łatwiej je odebrać. Mniejsza średnica tłoka skutkuje mniejszą siłą na niego działającą, przez co obciążenie korbowodu i wału korbowego również jest mniejsze. Z kolei mniejsza prędkość obrotowa nie wymaga tak precyzyjnego projektowania i obróbki ruchomych elementów.

S2000 vs. 350Z

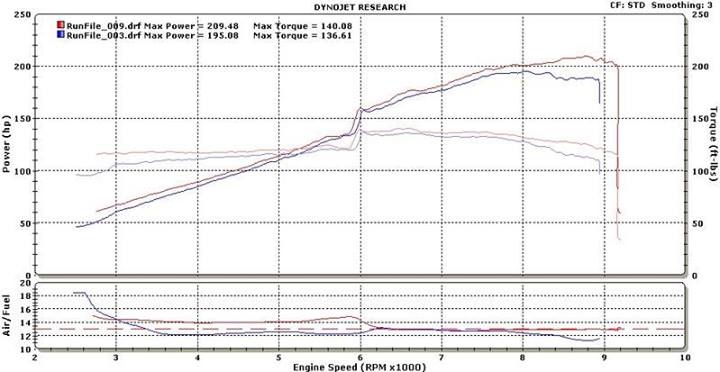
Weźmy na tablicę wysokoobrotowca z Hondy S2000 pierwszej generacji:

2l R4
247 KM @ 8300 rpm
218 Nm @ 7500 rpm
współczynnik kształtu cylindra: 1.046
~1250 kg
0-100 km/h w 6,2 sekundy
Vmax 241 km/h

Charakterystyka silnika – Honda S2000, źródło: Internet

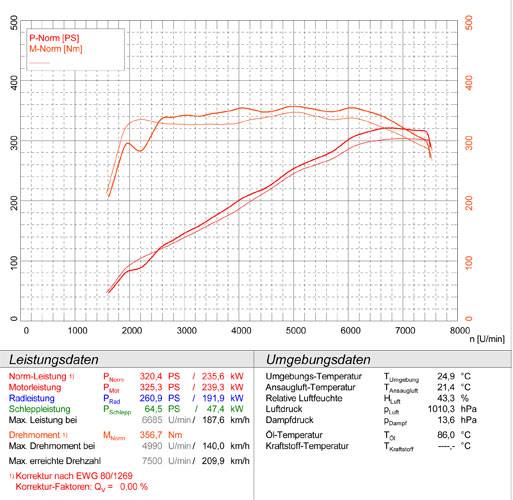
i wolnoobrotowy silnik z Nissana 350Z:

3,5l V6
310 KM @ 6800 rpm
364 Nm @ 4800 rpm
współczynnik kształtu cylindra: 1.17
~1450 kg
0-100 km/h w 5,8 sekundy
Vmax 249 km/h

Charakterystyka silnika – Nissan 350Z, źródło: Internet

Wartości z wykresów mogą się nieznacznie różnić od danych katalogowych. Wynika to z różnych warunków pomiarów, zużycia silnika, różnicach w specyfikacji paliwa itp. Poza tym te przedstawione tutaj nie zaczynają się od obrotów biegu jałowego. Charakterystyki silników przedstawione wyżej ściągane są poprzez pomiar siły na kołach na najczęściej 4. biegu. Silnik pracuje na minimalnych obrotach na tym biegu, a następnie wciskany jest gaz do dechy i trzymany aż do odcięcia. Stąd ta gwałtownie narastający moment obrotowy na początku oraz różnie umiejscowiony początek charakterystyki, aby nie przeciążać silnika. Po osiągnięciu maksymalnych obrotów silnik jest odłączany od skrzyni biegów (wrzucany jest luz) i hamownia mierzy straty w układzie przeniesienia napędu. Wynik to moc na kołach liczona jako iloczyn siły i prędkości minus moc potrzebna na pokonanie oporów układu przeniesienia napędu, czyli iloczyn siły oporów i prędkości:
$P_{{silnik}}=F_{{kola}} \cdot V - F_{{oporow}} \cdot V$

Powyższy wzór opisuje moc mierzoną na wale korbowym, ale tak ogólnie moc można też rozumieć jako iloczyn siły z jaką odpychają się koła i prędkości samochodu – wtedy będzie to moc na kołach, a nie moc silnika. Siła na kołach to po prostu moment obrotowy silnika zwiększony przez przekładnie i zmodyfikowany przez wielkość kół.

Z powodu niższego momentu obrotowego silnik S2000 wydaje się gorszy? Niekoniecznie – wyższa prędkość obrotowa pozwala zastosować większe przełożenie, przez co na koła trafia większy moment obrotowy. Gdyby pierwszy bieg kończył się na 100 km/h, to mimo o 34,7% mniejszego momentu obrotowego silnika Hondy przy mocy maksymalnej (209 Nm vs. 320 Nm), na kołach miałaby ona tylko o 20,3% mniejszy moment obrotowy (po przeliczeniu: 1903 Nm vs. 2388 Nm).

Ferrari 458 Italia, źródło: Internet

Ciekawostka

Z silników o takiej samej mocy dostępnej przy różnej prędkości obrotowej moment trafiający na koła będzie identyczny na przełożeniach o identycznej długości.

Moment na kołach wyrażamy jako:
$M_{kola} = M_{silnika} \cdot ratio$
M_koła – moment obrotowy na kołach (Nm)
M_silnika – moment obrotowy silnika (Nm)
ratio – przełożenie

A moc silnika jako:
$P_{silnika} = M_{silnika} \cdot 6,28 \;rad \cdot f_{silnika}$
P – moc silnika (W)
M_silnika – moment obrotowy silnika (Nm)
f_silnika – ilość obrotów na sekundę silnika (rps, Hz)

Przekształcając ten wzór możemy otrzymać:
$M_{silnika} = \frac{P_{silnika}}{6,28 \; rad \cdot f_{silnika}}$

Podstawiamy do wzoru na moment na kołach:
$M_{kola} = \frac{P_{silnika}}{6,28 \; rad \cdot f_{silnika}} \cdot ratio$

Przełożenie to stosunek prędkości obrotowej silnika do prędkości obrotowej kół:
$ratio = \frac{f_{silnika}}{f_{kola}}$

Zatem:
$M_{kola} = \frac{P_{silnika}}{6,28 \; rad \cdot f_{silnika}} \cdot \frac{f_{silnika}}{f_{kola}}$

Po skróceniu f_silnika:
$M_{kola} = \frac{P_{silnika}}{6,28 \; rad \cdot f_{kola}}$
$M_{kola1} = \frac{P_{silnika1}}{6,28 \; rad \cdot f_{kola1}}$
$M_{kola2} = \frac{P_{silnika2}}{6,28 \; rad \cdot f_{kola2}}$

Czyli jeśli P1 = P2 i fk1 = fk2, to Mk1 = Mk2. Założyłem, że obwód kół jest identyczny.

Zatem jeśli prędkość obrotowa koł zasilanych dwoma różnymi silnikami o identycznej mocy jest taka sama, to moment na nich również jest taki sam, mimo tego, że moment generowany przez silnik w punkcie maksymalnej mocy jest diametralnie różny.

Przykład?

Ferrari 458 Italia
570 KM @ 9000 rpm
Przy 9000 rpm generuje 444,92 Nm, co przy pierwszym biegu ciągnącym się do 100 km/h oznacza 4392 Nm na kołach.

Chevrolet Camaro ZL1
580 KM @ 6000 rpm
Przy 6000 rpm generuje 679 Nm, co w takiej samej konfiguracji, jak z Ferrari 458 Italia daje 4469 Nm na kołach.

1,75% większa moc w Camaro i 1,75% większy moment obrotowy na kołach. Dowiedz się więcej na ten temat i przeprowadź symulację w kalkulatorze we wpisie Z jaką siłą odpychają się koła?

Chevrolet Camaro, źródło: Internet

Przyśpieszenie i jazda na niskich obrotach

Duża różnica momentu obrotowego zasadniczo wpływa na styl jazdy. Najlepsze są silniki z płaskim przebiegiem momentu obrotowego – w przypadku zmniejszenia prędkości, skutkującej zmniejszeniem prędkości obrotowej silnika nie ma potrzeby redukować biegu, gdyż moment będzie taki sam. Wszak to moment obrotowy jest siłą trafiającą na koła. Wobec tego nie zastanawiałeś się dlaczego samochód z płaskim przebiegiem lepiej przyśpiesza na górze mimo, że wg. tego, co mówię powinien jednakowo przyśpieszać w pełnym zakresie prędkości obrotowej? Różnica pochodzi z przełożeń skrzyni biegów. Przyśpieszając na 5 biegu z 2000 rpm na koła trafia znacznie mniejszy moment niż na 3 biegu przy 5000 rpm mimo jednakowego momentu obrotowego z silnika. Przełożenie niższego biegu jest większe, co pozwala uzyskać większy moment obrotowy na kołach.

Lepszy jest silnik, w którym biegami reguluje się tylko przyśpieszenie, od silnika któremu obroty trzeba utrzymywać w pewnym wąskim zakresie. Stąd też przewaga silników wolnoobrotowych. Charakteryzują się one większym momentem obrotowym i znacznie lepszym dołem. Potężne silniki potrafią pracować już przy 400 rpm. Lata ’70 ubiegłego wieku i Chervolet Corvette C3 z 7l silnikiem V8, który przy 800 rpm dysponował prawie 550 Nm! Nowym Camaro z 6,2 litrową V8 da się ruszyć płynnie z miejsca startując z 400 rpm na 4 biegu!

Charakterystyki silnika – Chevrolet Corvette C3 (1970), źródło: Internet

Gama silnikowa – Chevrolet Corvette C3

Wysokoobrotowa charakterystyka silnika

Często wysokoobrotowe silniki mają słaby dół, przez co jazda w tym zakresie powoduje pracę silnika z mniejszą sprawnością, co przekłada się na duży wzrost zużycia paliwa. Zwiększenie prędkości obrotowej silnika do zakresu, w który ma on wysoki moment obrotowy powoduje zwiększenie jego sprawności, ale powoduje również wzrost jego oporów wewnetrznych, na pokonanie których również zużywane jest paliwo.

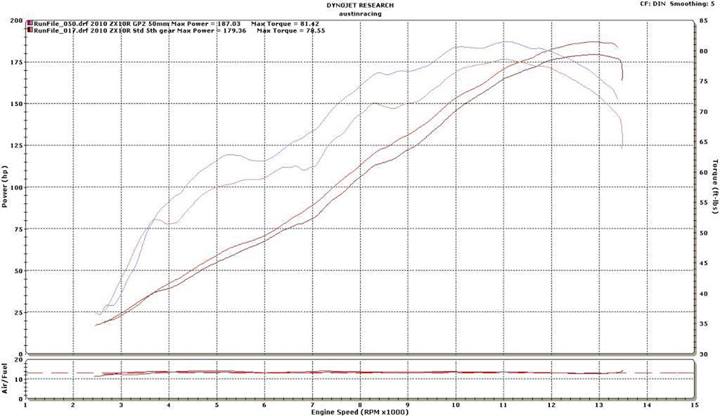
Poniżej charakterystyka silnika Kawasaki ZX-10R:

Charakterystyka silnika Kawasaki ZX-10R, źródło: Internet

Jeśli przy 11000 rpm osiąga on 20% sprawności, to przy 3000 rpm posiada ponad dwukrotnie mniejszy moment obrotowy, przez co jego sprawność spada o połowę, do ~10%. Jeśli przy jeździe ze stałą prędkością przy 10000 rpm spalałby 4 l/100 km, to przy jeździe z taką samą prędkością, ale na wyższym biegu, mając 3000 rpm zużycie wzrosłoby do ~8 l/100 km.

Nie da się jednoznacznie określić, która charakterystyka silnika jest lepsza. Jedna i druga ma swoich zwolenników i przeciwników, jedna i druga filozofia ma swoje wady i zalety. Silniki wolnoobrotowe z pewnością są bardziej uniwersalne i lepsze do normalnej eksploatacji. Jednak gdy w grę wchodzi redukcja masy lub mała ilość miejsca na silnik wtedy na znaczeniu zyskują silniki wysokoobrotowe.

Michał Michna

Blog stworzony, by dać ujście pasji do motoryzacji i techniki, a także…

Widgets

Search

O mocy i momencie obrotowym…